Comb-drive actuator design
We consider the case depicted in Figure 1 of a comb-drive
actuator. This actuator is the favored electrostatic actuator for its relative
large range and good force/electrical power ratio. It is composed of N
fingers on the rotor that are interleaved with the N+1 fingers of the stator.
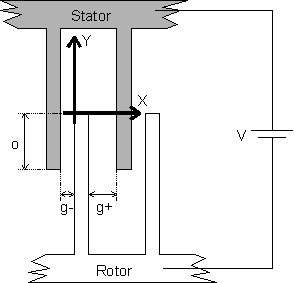 Figure 1: View of one period of an electrostatic
comb-drive actuator
Figure 1: View of one period of an electrostatic
comb-drive actuator
We want to know the force attracting the electrodes when
we apply a voltage. We will obtain this force via the differentiation of
the expression of the energy stored in the system.
I Electrostatic force
In order to derive the mechanical force generated by the
electrostatic actuator we will differentiate the work of the force i.e.,
the energy stored in the system. The energy stored in a capacitor is given
by:
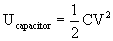 (1)
(1)
The total energy stored in the circuit is given by the
energy stored in the capacitor minus the energy taken from the power source
to charge it, that is:
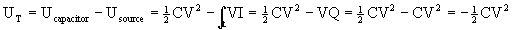 (2)
(2)
We simplify the computation of the capacitance by considering
only the lateral surfaces of neighbor fingers. We neglect the interaction
with the part of the finger that is not engaged and with the horizontal
surfaces (the fingers are considered infinitely thin). Moreover, we neglect
the presence of the other fingers and the effects arising at the comb edge.
Using this simplification, we may compute the capacitance of the comb by
summing N times the capacitance of one finger. We describe a finger as
two planar capacitors in parallel (one per side), and neglecting the fringing
fields, we have:
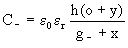 (3)
(3)
and:
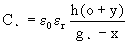 (4)
(4)
where the variable and constant are shown in Figure 2.
Hence the capacitance of the comb is:
C = N Cfinger = N (C- + C+)(5)
I.1 Longitudinal force (i.e., parallel to the finger)
This force may be assessed by:
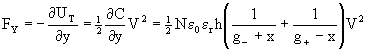 (6a)
(6a)
if the two lateral gaps are equal, g+ = g-
= g, and x = 0, we may simplify this expression and obtain:
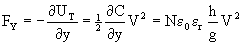 (6b)
(6b)
I.2 Lateral force (i.e., perpendicular to the finger)
This force is given by:
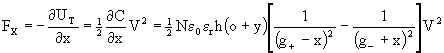 (7)
(7)
If the two lateral gaps are equal and x = 0, the two lateral
force are equal and the resultant net force along the X-axis is nearly
zero. However, when x is different from zero, this lateral force may lead
to instability when it increases more rapidly than the restoring lateral
elastic force, bringing finger into contact. In a similar way, this effect
may bend thin and long fingers causing short-circuit. This effect will
be described in the next section.
To be complete, if there is only one side of the finger
experiencing the electrostatic force, as in a gap-closing actuator, the
expression simplifies slightly and yields:
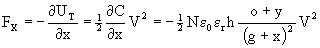 (8)
(8)
II Displacement
The comb-drive principle seems to allow displacement only
limited by the length of the finger. Actually, for any voltage greater
than zero there will be a longitudinal force that will pull the rotor toward
the stator continuously. This may be true in some extent for a guided slider,
provided a scheme for biasing has been found and the electrostatic force
overcomes the friction force. However, these two later points are generally
solved by suspending the rotor above the substrate, limiting the achievable
displacement. Actually, the suspension creates mechanical force acting
against the displacement and the net displacement is obtained when the
electrostatic force is equal to this mechanical force. The suspension presents
the benefit to bring the rotor to its original position when the voltage
(i.e., the electrostatic force) is decreased to zero. Thus, the displacement
is limited by the maximal electrostatic force that may be obtained, which
in turn is limited by the maximum voltage that can be applied. We will
further see that the suspended rotor is subject to lateral instability
that limits this voltage, much before the ionization of the insulator between
the rotor and the stator appear.
II.1 Limitation imposed by the suspension
The suspension of the rotor creates a force FmY
acting against the displacement along Y-axis that is given by:
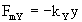 (9)
(9)
where kY is the spring constant of the suspension
along the Y axis (i.e., the linear elastic constant), the suspension being
not deformed when y = 0. Then the static displacement of the rotor is obtained
by writing the equilibrium of the mechanical and electrostatic forces.
Taking the case g+ = g- = g, and er=1
(air) we have:
 (10)
(10)
Example 1:
With an air gap of 2 µm width, electrodes height of 2 µm
and 10 µm of engaged electrodes we have:
FY = N* 8.85·10-12 * 2·10-6
/ 2·10-6 = N*8.85·10-12 N/V2
thus it is about 0.008 µN by finger for an applied
voltage of 30 V.
For the first application of the movable mirror we need
a displacement of the order of l/2 (~0.5 µm).
For a suspension with a spring constant of 1 N/m and with an applied voltage
of 30V, we need at least 60 fingers. To obtain the displacement of several
µm needed for the second application, we may either increase the
number of finger or decrease the spring constant. With the same actuator
and a spring constant of 0.16 N/m, the actuation range becomes 3 µm.
For this voltage, the force generated by the actuator
will be 0.48 µN. For example this correspond to an acceleration of
100 g applied on a mass of 0.5·10-9
kg. This value is a good estimate of the maximum range obtained when the
actuator is used as a force feedback in an accelerometer, provided
the actuator is not deflected in the reference position. In that latter
case the maximum available force will be decreased by the reaction of the
suspension at the 'rest' position. To account for random direction acceleration,
a two-way actuator should be used.
II.2 Limitation imposed by lateral electrostatic instability
At first thought it seems that increasing the voltage on
the actuator will increase the displacement continuously. However, for
a high enough voltage the lateral electrostatic force increases more rapidly
than the restoring lateral elastic force when the finger moves laterally.
At this point any small initial lateral displacement will inexorably bring
neighbor fingers into contact. This critical voltage is formally given
by the comparison between the x-derivatives of the lateral electrostatic
force (i.e., ¶ Fx/¶
x) and the x-derivatives of the lateral mechanical force (i.e., the spring
constant along X, kX):
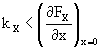 (8)
(8)
Taking the case g+ = g- = g, and
er=1 (air) this relationship becomes:
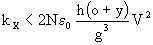 (9)
(9)
Thus, the maximum voltage, Vmax, that may be applied to
the actuator before instabilities occur is:
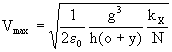 (10)
(10)
We see that this limit decreases with smaller gap and
with larger electrodes total lateral surface (i.e., N h (o + y)).
Example 1:
With an air gap of 2 µm width, electrodes height
of 2 µm and 10 µm of engaged electrodes we have a lateral force
on each surface, determined using (8):
FX = -.5 * 8.85·10-12 *
2·10-6 *10·10-6 / 4·10-12
= 2.21·10-11 N/V2
thus it is about 0.02 µN for an applied voltage
of 30 V
For a full rotor finger, with the same gap on both side,
the same force apply on each lateral surface, therefore in the ideal case,
neither a bending moment nor a lateral force should appear as can be computed
from (7). However, this equilibrium is unstable as soon as the voltage
exceeds the critical voltage. To compute this voltage it is necessary to
observe that the lateral stiffness of the suspension is much lower when
the suspension is deflected. Thus for y=0, a typical folded beam suspension
with 300 µm-long beams has a spring constant of kX = 2Ehw/l
= 4533 N/m . However when y>0, the spring constant becomes kX
= 5.5 E h w3/Lx2,
thus kX = 503 N/m for a 10 µm deflection and kX
= 125 N/m for a 20 µm deflection. The corresponding critical voltages
for a 60-fingers comb-drive are, respectively:
Vmax = 1306 V, 308 V, and 124 V.
It is apparent that this limitation becomes a real problem
for actuator with large range of displacement.
III References
W. Tang, T. Nguyen, and R. Howe, "Laterally driven polysilicon
resonant microstructures", Sensors and actuators, Vol. 20, pp. 25-32, 1989
W. C. Tang, "Electrostatic comb-drive for resonant sensor
and actuator applications", PhD thesis, University of California, Berkeley,
1990
R. Legtenberg, A. Groeneveld and M. Elwenspoek, "Comb-drive
actuators for large displacements", J. Micromech. Microeng. Vol. 6, pp.
320-329, 1996


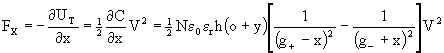 (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
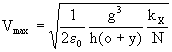 (10)
(10)